Disc packing problem: Testing of the circular boundary code for Voronoi diagrams
Our prototype code is running. But did we cover all special cases and does it work with more than a handfull of data points?
At first I checked for the special cases the naive math programmer forgets.
Most people learn in the high school that a line is defined by the equation :
y = m * x + b
and for two given points (A.x, A.y) and (B.x, B.y) the paramters m and b can be derived as
m = (A.y-B.y)/(A.x-B.x)
b = A.y - m * A.x
This is correct for most of the lines, but not for a vertical line. In this case you will get a "division by zero" error from the derivation of m since (A.x-B.x) is zero.
The mathematicans have brought us a generalisation of the line equation:
a * x + b* y = c
For horizontal lines we have
a = 0
b = 1
and c = A.y
For vertical lines we have
a = 1
b = 0
and c = A.x
For all the other (common) lines with b=1 we get y = -a*x +c where -a equals m of the high school formula.
So at first we test our code for horizontal and vertical edges.
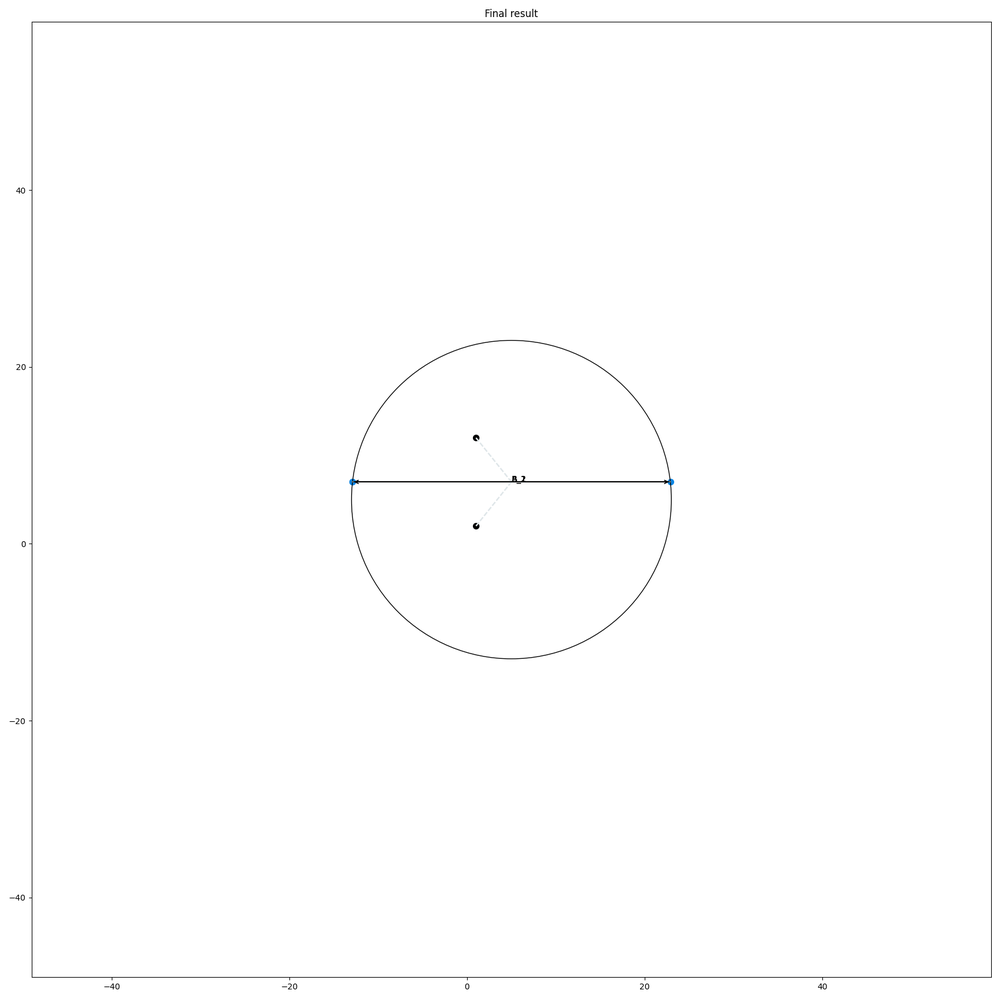
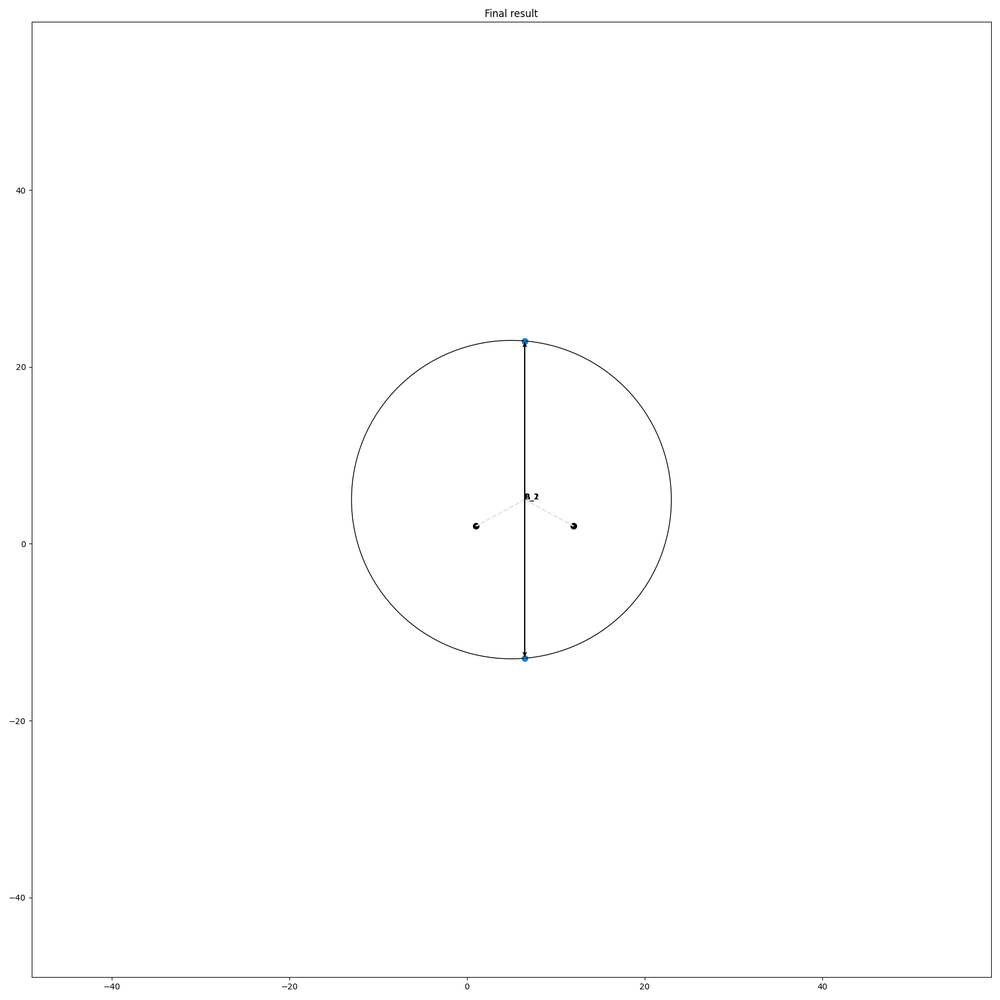
Works like a charm.
Next we tested for many datapoints. The Voronoi code of the original author is only a showcase and not meant for speed.
So we do not do any benchmarks, this can be done later. We were just interested to test if the algorithm and our extension breaks by the variety of cases.
A Voronoi diagram of 1000 data points gaussian distributed and centered on our clipping circle:

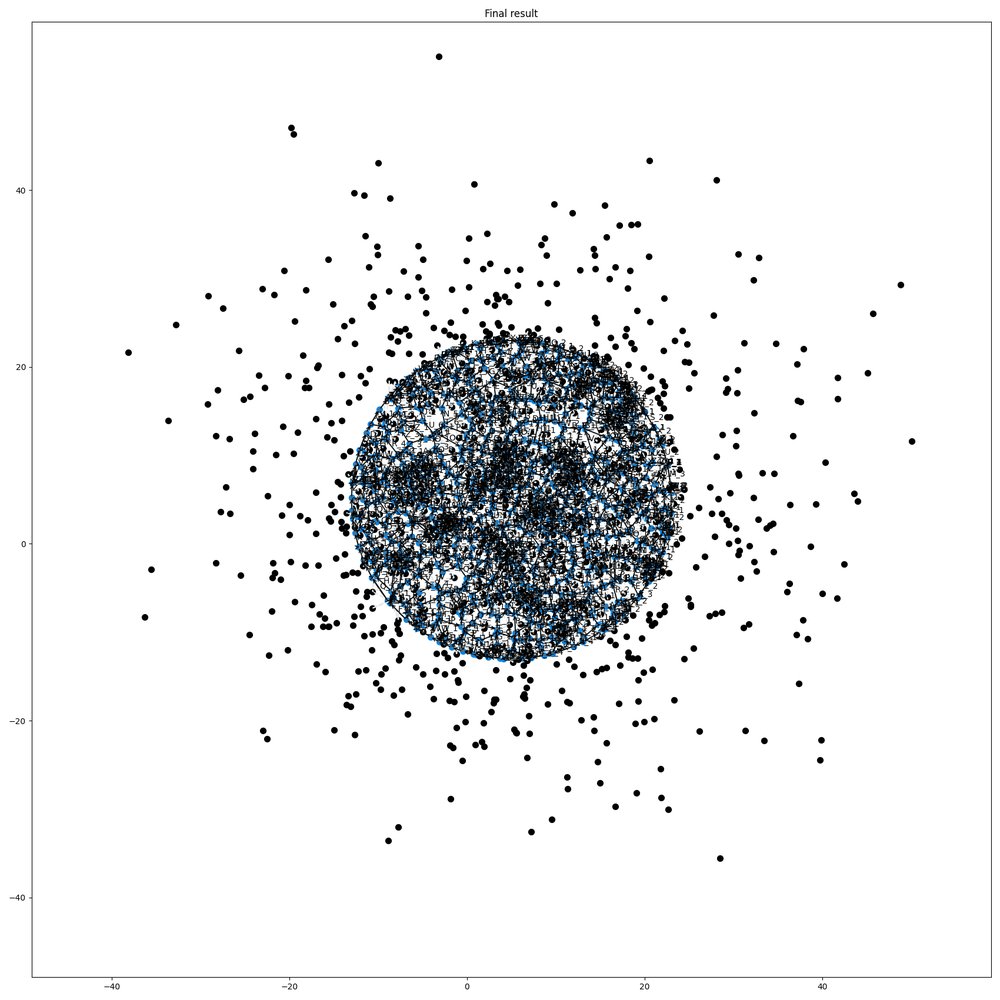
And the final clipped Voronoi diagram.
The keen observer may have noticed the lower density in the clipped diagram. This is due to the fact that a lot of outyling incidence points no longer contribute to the voronoi diagram.
I am quite happy with this. For the final goal of the algorithm there will never be points outside the boundary circle. But I like to programm as robust as possible.
Now I can derive the seed Voronoi-Diagram for the disc-Problem which I need for the second step of the paper I like to implement.
