Apollonius tenth problem: Tangent circle to three other circles: Effectively solved by moebius transformation

I found an interesting article [1] that tackles this problem utilizing a moibius transformation and thus solves it analytically.

Asume we have three circles C1,..,C3.

The really cool idea of this paper is to shrink (better term maybe substract of) the radii of the circles so that one radius becomes zero: Let's assume it is C1. So we got C1 with a radius of zero.

Then we transform the euclidian plane so that C1 is in the origin of a new complex plane Z. Then we transform Z with a moibius Z->1/Z tranformation opbtaining a new Plane W.

In the W-Plane C1 is pushed to infinity leaving only C2-> W2 and C3 -> W3 as circles. If we now construct tangents T1 and T2 on W2 and W3. T1, T2 are touching W2 and W3 and since they are infinite lines touching infinity (the transformed C1). After an appropriate back moibius transformation W->1/W the former tangents become the Appolonius circles we are looking for.

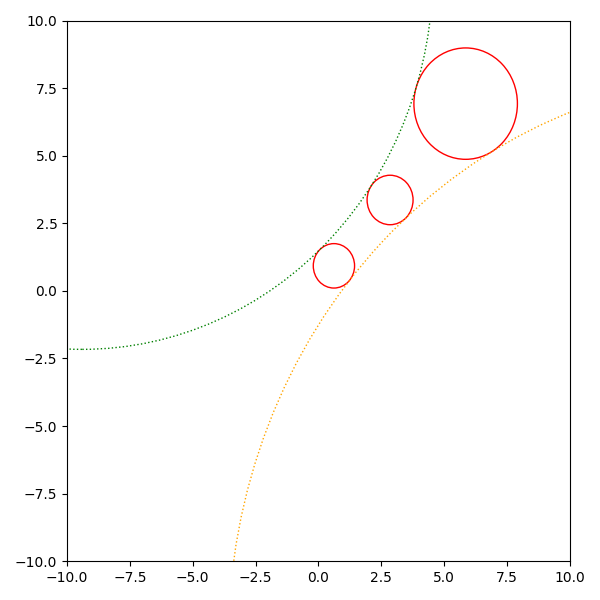
Colored red the three circles we like to have a tangent circle for an in green and orange the Apollonius tangent circles.

There may be two (seen above), one (below), or zero (below, below) solutions.

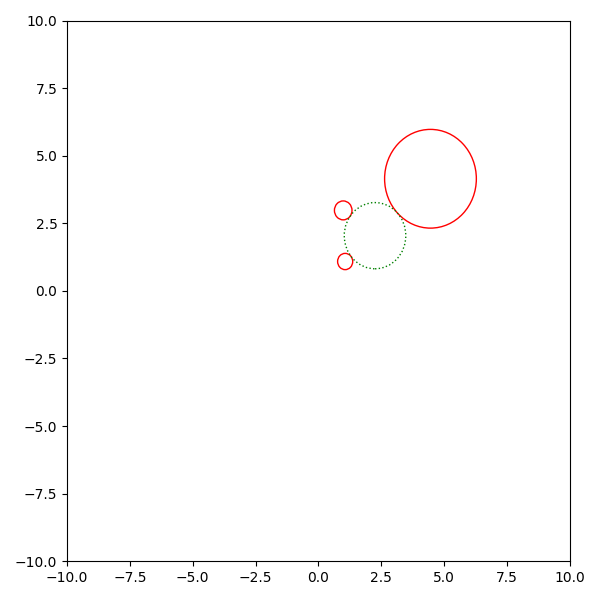
In this case no tangent circle can be constructed.

import math
from random import random
import matplotlib.pyplot as plt
from datetime import datetime

fig, ax = plt.subplots(figsize=(6, 6))
ax.set(xlim=(-10, 10), ylim=(-10, 10))

EXACT = 1e-10

class Circ(object):
 def __init__(self, x, y, r):
 self.x = x
 self.y = y
 self.r = r

@classmethod
 def rand(self, rand_xy, rand_r):
 circ = Circ(
 random() * rand_xy,
 random() * rand_xy,
 random() * rand_r
 )
 return circ

def shrink(self, amount):
 return Circ(self.x, self.y, self.r-amount)

def distance(self, c):
 distance = math.sqrt((self.x-c.x)**2 + (self.y-c.y)**2) - self.r -c.r
 return distance

def overlap(self, c):
 return self.distance(c) < 0

class Tangent(object):
 def __init__(self, a, b, c):
 self.a = a
 self.b = b
 self.c = c

def backtransform(self, c1):
 a = self.a/self.c
 b = self.b/self.c

return Circ(
 c1.x -a/2.,
 c1.y +b/2,
 math.sqrt(a**2 + b**2)/2 - c1.r
 )

def tangets(circ1, circ2):
 dx = circ2.x - circ1.x
 dy = circ2.y - circ1.y
 dr = circ2.r - circ1.r

D = math.sqrt(dx * dx + dy *dy)
 X = dx/D
 Y = dy/D
 R = dr/D

a1 = R * X - Y*math.sqrt(1 - R*R)
 b1 = R * Y + X*math.sqrt(1 - R*R)
 c1 = circ1.r - (a1*circ1.x + b1*circ1.y)

a2 = R * X + Y*math.sqrt(1 - R*R)
 b2 = R * Y - X*math.sqrt(1 - R*R)
 c2 = circ1.r - (a2*circ1.x + b2*circ1.y)

return Tangent(a1, b1, c1), Tangent(a2, b2, c2),

def moebius_transform(circ):
 D = (circ.x-c1.x)**2 + (circ.y-c1.y)**2 - circ.r**2
 xr = (circ.x-c1.x)/D
 yr = -(circ.y-c1.y)/D
 rr = circ.r/abs(D)
 return Circ(xr, yr, rr)

def point(a,b,c,x):
 return (-c-a*x) / b

def plot_tangents(tgs):
 for tg in tgs:
 ax.axline(
 (0, point(tg.a, tg.b, tg.c,0)),
 (10, point(tg.a, tg.b, tg.c,10)),
 color="black")

def plot_circ(circ, **kw):
 return plt.Circle((circ.x, circ.y), circ.r, **kw)

c1 = Circ.rand(5,3)
while True:
 c2 = Circ.rand(5,3)
 if not c2.overlap(c1):
 break
while True:
 c3 = Circ.rand(8,4)
 if not (c3.overlap(c1) or c3.overlap(c2)):
 break

circles = [c1, c2, c3]

c2_shrunk = c2.shrink(c1.r)
c3_shrunk = c3.shrink(c1.r)

circ1 = plot_circ(c1, color='r', fill=None)
circ2 = plot_circ(c2, color='r', fill=None)
circ3 = plot_circ(c3, color='r', fill=None)

ax.add_artist(circ1)
ax.add_artist(circ2)
ax.add_artist(circ3)

#circ2_shrunk = plot_circ(c2_shrunk, color='r', fill=None, ls='--')
#circ3_shrunk = plot_circ(c3_shrunk, color='b', fill=None, ls='--')

#ax.add_artist(circ2_shrunk)
#ax.add_artist(circ3_shrunk)

tgs = tangets(moebius_transform(c2_shrunk),
 moebius_transform(c3_shrunk))

A1 = tgs[0].backtransform(c1)
A2 = tgs[1].backtransform(c1)

good = True
for c in circles:
 dist = c.distance(A1)
 if dist < -EXACT or dist > EXACT:
 good = False
 break

if good:
 circ_A1 = plot_circ(A1, color='g', fill=None, ls=':')
 ax.add_artist(circ_A1)

good = True
for c in circles:
 dist = c.distance(A2)
 if dist < -EXACT or dist > EXACT:
 good = False
 break

if good:
 circ_A2 = plot_circ(A2, color='orange', fill=None, ls=':')
 ax.add_artist(circ_A2)

fig.show()

with open(str(datetime.now())+'.png', 'wb') as outfile:
 fig.savefig(outfile)

This code is crap and was never meant for anything than the dump. But it shows the prove of concept.

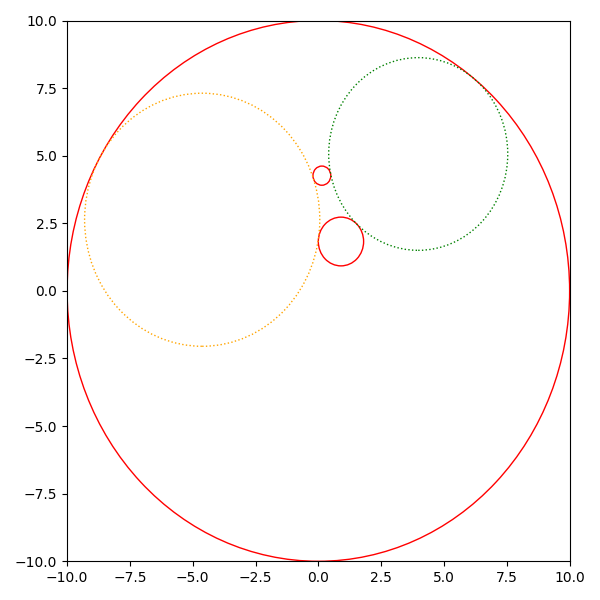
The above algorithm can be modified to also solve the problem of a tangent circle of two circles in an enclosing circle. This is vital for algorithms of disc packaging into a circle.

 [1] https://www.sciencedirect.com/science/article/abs/pii/S0010448505001016